주어진 숫자 X를 1로 만드는 데 연산을 사용하는 횟수의 최솟값을 출력하는 문제다.
연산은 세 가지만 사용할 수 있다.
1) X가 3의 배수면 3으로 나눈다.
2) X가 2의 배수면 2로 나눈다.
3) 1을 뺀다.
처음에는 우선순위를 두고 그리디 방법으로 풀었더니 오답이 나왔다.
질문란에 가니 나같은 사람이 많았다 ^_ㅠ...
반례에 대한 질문의 답을 보니 3k+1 꼴일 때,
1을 빼고 3으로 나누는데 2로 나누는 것보다 항상 적게 걸린다고 할 수 없기 때문이라는 듯하다.
반례가 참 많았다.. 따라서 그리디로는 풀 수 없는 문제!
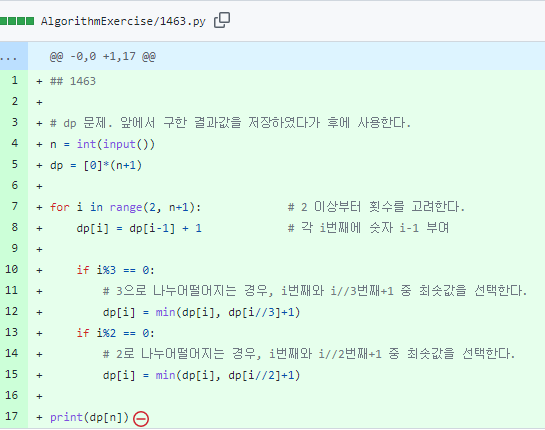
dp라는 배열을 만들어주고, i번째에 숫자 i-1을 부여한다.(아무 조건이 없을 때만.)
아래의 조건문에서 걸리면 숫자가 i-1이지만은 않다.(예시 참고)
dp=[0]*(n+1)로 선언한 뒤 반복문 내에서 dp[i] = dp[i-1]+1로 부여해주면 된다.
피보나치 수열과 유사처럼, 앞의 항이 그 뒤의 항에 영향을 주는 방식이다.
3으로 나누어떨어지는 경우에는 dp의 i//3번째 +1과 i번째 중 작은 값을 선택한다.
2로 나누어떨어지는 경우에는 dp의 i//2번째 +1 과 i번째 중 작은 값을 선택한다.
이후 dp[n]을 출력해주면 된다.
n=2 이면, dp[2] = 1, dp[2//2]+1 = dp[1]+1 = 1이다.
둘 중 min 값을 선택하면 둘다 1이므로 어쨌든 1이 된다.
n=3이면, dp[3] = dp[2]+1 = 2, dp[3//3]+1 = dp[1]+1 = 1이다.
둘 중 min 값을 선택하면 1이 된다.
n=4이면 dp[4] = dp[3]+1 = 2, dp[4//2]+1 = dp[2]+1 = 1+1 = 2이다.
둘 중 min 값을 선택하면 둘다 2이므로 어쨌든 2가 된다.
n=5이면, dp[5] = dp[4]+1 = 3, 그리고 3과 2 중 나누어떨어지는 숫자가 없으므로 그냥 3이 된다.
실제로 계산해보면 5에서 1을 빼서 4가 되고, dp[4]=2이므로 총 3이다.
조건문 내에 1을 빼주는 연산은 dp[i] = dp[i-1] + 1에 포함되었음을 알 수있다.
'공부 > 백준' 카테고리의 다른 글
| [백준] 2460번 (0) | 2022.06.15 |
|---|---|
| [백준] 25191번 (0) | 2022.06.15 |
| [백준] 5566번 (0) | 2022.06.15 |
| [백준] 2753번 (0) | 2022.06.15 |
| [백준] 1929번 (0) | 2022.06.15 |



