이전에 푼 요세푸스 문제를 풀었다면 큐로 푸는 것은 어렵지 않다.
하지만 문제를 읽는 중 규칙을 발견해서, 조금 돌아가서 빠르고 정확한 사칙연산 문제로도 풀어보았다.
우선 큐, 덱을 이용한 정석적인 풀이다.
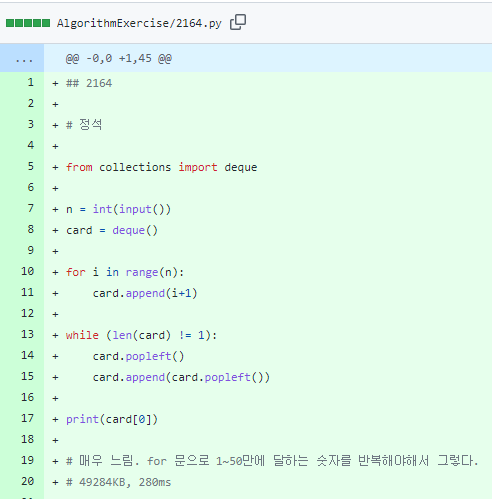
구현 자체는 눈으로 봐도 쉽게 이해가 된다. 요세푸스 문제에서 다룬 것이기 때문에..
문제에서 말한대로 처음 시작할때 맨 위의 장을 버리고(popleft), 그 다음 장은 맨 뒤로 넣는다(append)
그걸 카드가 한 장 남을 때까지(while (len(card) !=1)) 반복해주면 된다.
그러나...
n의 범위가 1부터 500,000 까지이기 때문에 n이 높은 숫자일수록
반복문이 돌아가는 횟수가 아주 많아지므로 속도가 느려질 수밖에 없다.
그래서 고민하며 메모장에 결과를 작성해보던 도중 결과값의 규칙을 찾아냈다.



난 멍청하기 때문에... 하나하나 다 적어보며 계산해봤다. 그렇다 노가다를 했다.
틀린게있을수도 있다
메모장에 써내려간 것처럼, 어느 순간 보면 홀수는 다 사라지고 짝수만 오름차순으로 정렬되는 것을 볼 수 있다.
당연하다. 1을 버리고 시작했고, 그 뒤로 2개의 숫자 간격으로 버리니 홀수가 다 사라진다.
그리고 짝수의 값을 뒤로 차례로 옮겼으니 짝수의 값이 오름차순 되어 정리된다.
거기까지 발견한 건 좋았다. 그 이후로 그래서 뭐? 상태가 됐다.
규칙을 발견한건 좋은데, 인적성 문제처럼 그 규칙으로 객관식 찍는 것도 아니고 어쩌라고...가됐다
:)...
한참 고민하고 식을 세워보다가 2의 n제곱 규칙을 찾아냈다.
주어진 값이 18일 경우를 가정해보자.
가장 근접하면서 작은 n제곱은 16이다. 이를 a 라는 값이라고 치자.
+ 참고로 밑에서 세번째 결과를 보자. 4와 12다. 두 수의 차는 a//2값이다. 사실 이 규칙을 식에 적용하진 못한거같다.
다시 돌아와서, 주어진 값 18에서 a인 16일 빼면 2가 된다. 여기서 2를 곱하면 4다.
이번엔 주어진 값이 17이라고 생각해보자. 17에서 a인 16을 빼면 1이 된다. 여기서 2를 곱하면 2다.
이번엔 주어진 값이 10이라고 생각해보자. 10에서 a인 8을 빼면 2가 된다. 여기서 2를 곱하면 4다.
어느정도 규칙이 눈에 익는다.
하지만 if문을 깔끔하게 쓰려면 이 2의 n제곱 값이 주어진 값보다 커지는 순간을 노리는 편이 훨씬 낫다.
그리하여 쓴 반복문
~
mag = 2
(while문 안에서)
mag *=2
if mag >= n:
~
그럼 속도도 훨씬 빠르고 그냥 사칙연산으로 풀 수있는 규칙 문제가 된다.

'공부 > 백준' 카테고리의 다른 글
| [백준] 5622번 (0) | 2022.06.16 |
|---|---|
| [백준] 20499번 (0) | 2022.06.16 |
| [백준] 2747번 (0) | 2022.06.15 |
| [백준] 10103번 (0) | 2022.06.15 |
| [백준] 7568번 (0) | 2022.06.15 |



